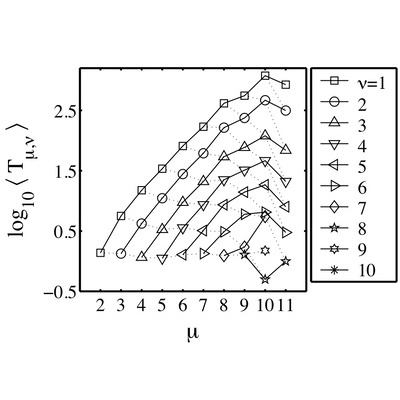
Essential to understanding the overall structure of river networks is a knowledge of their detailed architecture. Here, we explore the presence of randomness in river network structure and the details of its consequences. We first show that an averaged view of network architecture is provided by a proposed self-similarity statement about the scaling of drainage density, a local measure of stream concentration. This scaling of drainage density is shown to imply Tokunaga's law, a description of the scaling of side branch abundance along a given stream, as well as a scaling law for stream lengths. We then consider fluctuations in drainage density and consequently the numbers of side branches. Data is analyzed for the Mississippi River basin and a model of random directed networks. Numbers of side streams are found to follow exponential distributions as are inter-tributary distances along streams. Finally, we derive the joint variation of side stream abundance with stream length, affording a full description of fluctuations in network structure. Fluctuations in side stream numbers are shown to be a direct result of fluctuations in stream lengths. This is the last paper in a series of three on the geometry of river networks.