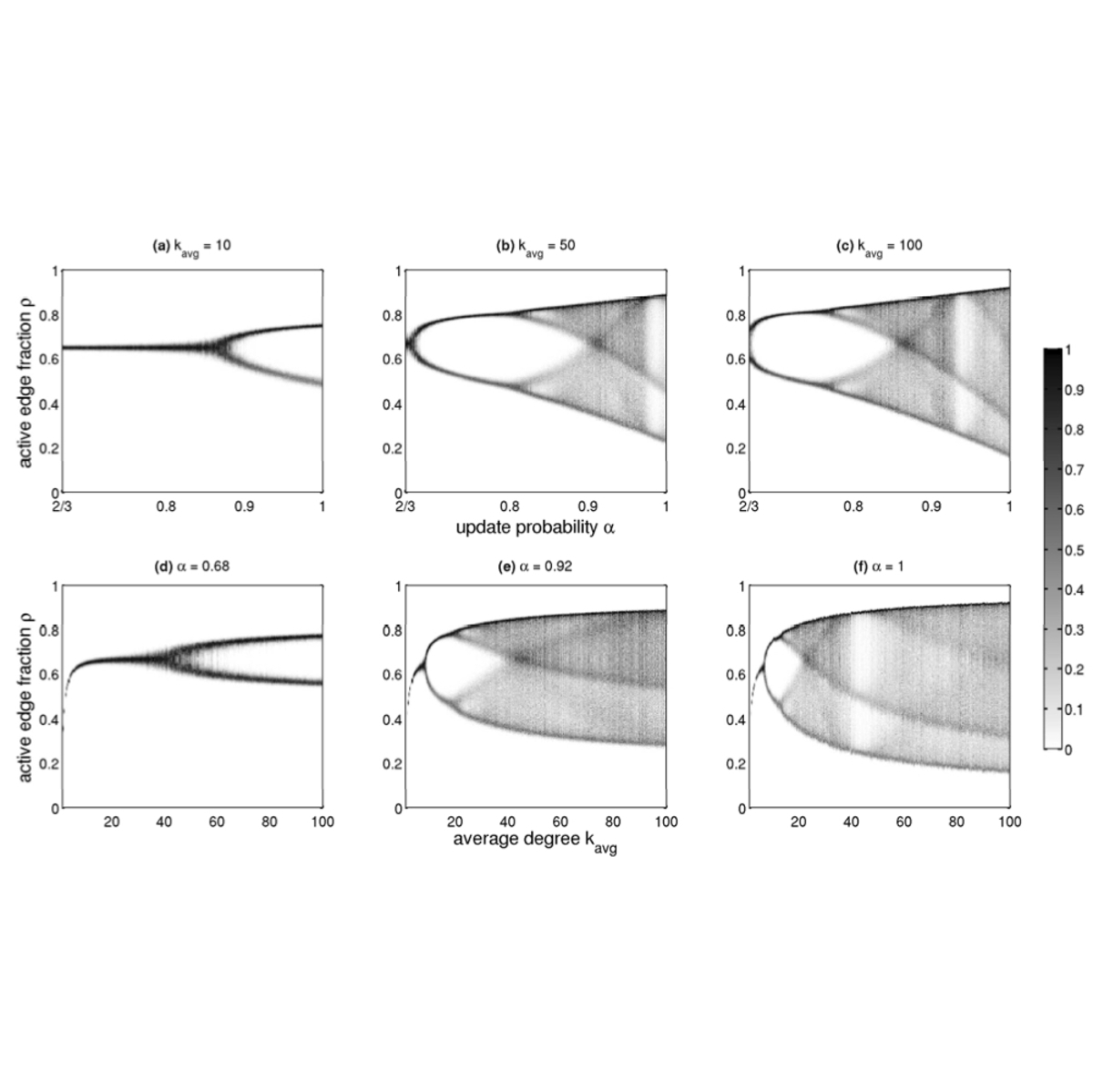
We study binary state dynamics on a network where each node acts in response to the average state of its neighborhood. Allowing varying amounts of stochasticity in both the network and node responses, we find different outcomes in random and deterministic versions of the model. In the limit of a large, dense network, however, we show that these dynamics coincide. We construct a general mean field theory for random networks and show this predicts that the dynamics on the network are a smoothed version of the average response function dynamics. Thus, the behavior of the system can range from steady state to chaotic depending on the response functions, network connectivity, and update synchronicity. As a specific example, we model the competing tendencies of imitation and non-conformity by incorporating an off-threshold into standard threshold models of social contagion. In this way we attempt to capture important aspects of fashions and societal trends. We compare our theory to extensive simulations of this "limited imitation contagion" model on Poisson random graphs, finding agreement between the mean-field theory and stochastic simulations.