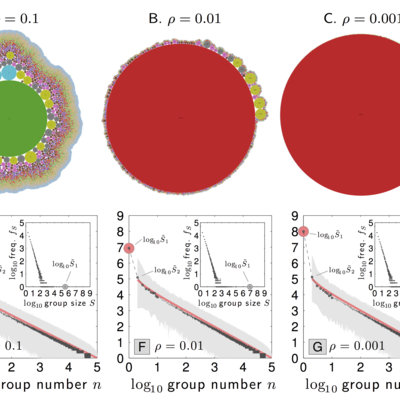
Herbert Simon's classic rich-get-richer model is one of the simplest empirically supported mechanisms capable of generating heavy-tail size distributions for complex systems. Simon argued analytically that a population of flavored elements growing by either adding a novel element or randomly replicating an existing one would afford a distribution of group sizes with a power-law tail. Here, we show that, in fact, Simon's model does not produce a simple power law size distribution as the initial element has a dominant first-mover advantage, and will be overrepresented by a factor proportional to the inverse of the innovation probability. The first group's size discrepancy cannot be explained away as a transient of the model, and may therefore be many orders of magnitude greater than expected. We demonstrate how Simon's analysis was correct but incomplete, and expand our alternate analysis to quantify the variability of long term rankings for all groups. We find that the expected time for a first replication is infinite, and show how an incipient group must break the mechanism to improve their odds of success. Our findings call for a reexamination of preceding work invoking Simon's model and provide a revised understanding going forward.