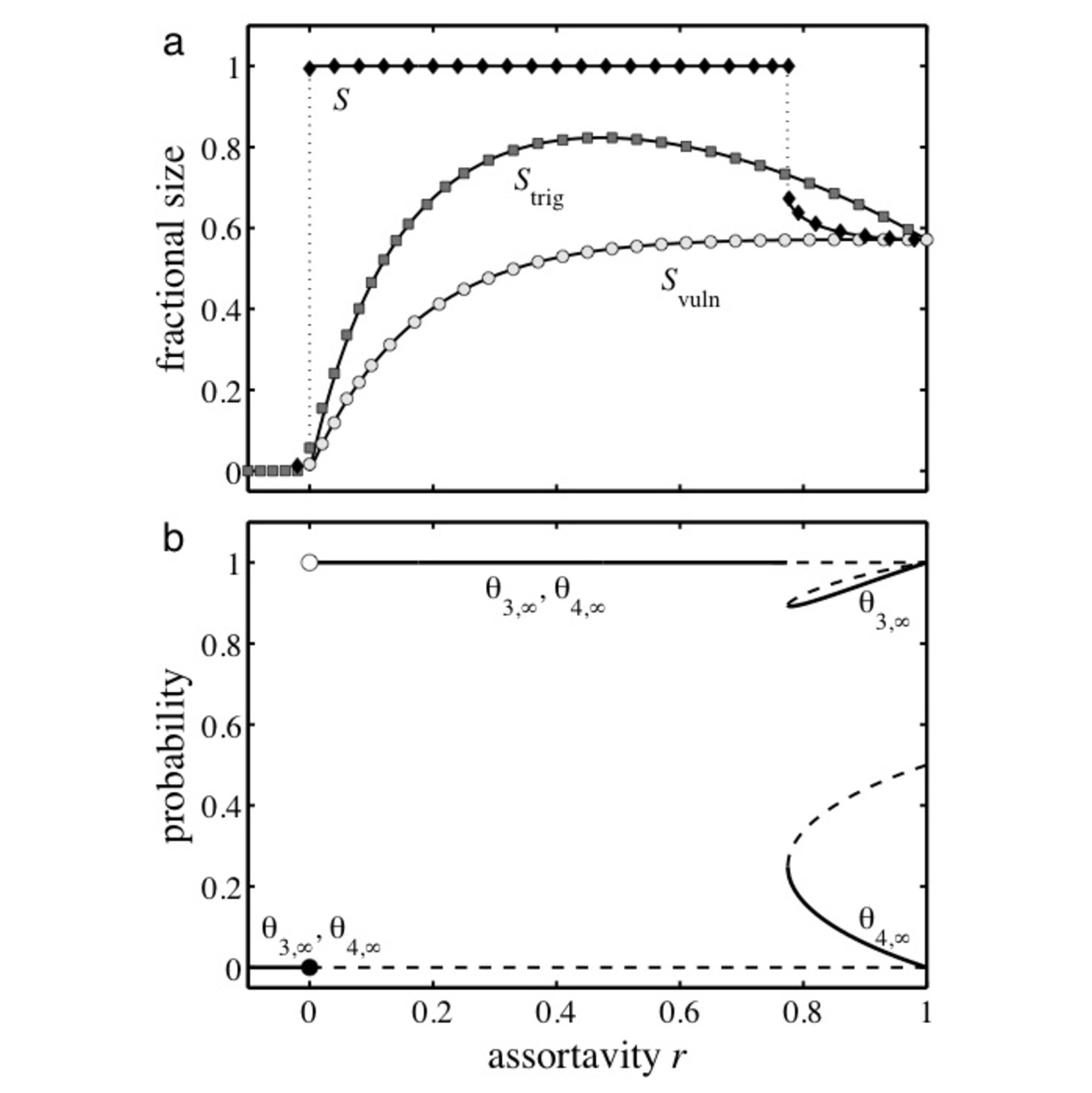
We analytically determine when a range of abstract social contagion models permit global spreading from a single seed on degree-correlated, undirected random networks. We deduce the expected size of the largest vulnerable component, a network's tinderbox-like critical mass, as well as the probability that infecting a randomly chosen individual seed will trigger global spreading. In the appropriate limits, our results naturally reduce to standard ones for models of disease spreading and to the condition for the existence of a giant component. Recent advances in the distributed, infinite seed case allow us to further determine the final size of global spreading events, when they occur. To provide support for our results, we derive exact expressions for key spreading quantities for a simple yet rich family of random networks with bimodal degree distributions.