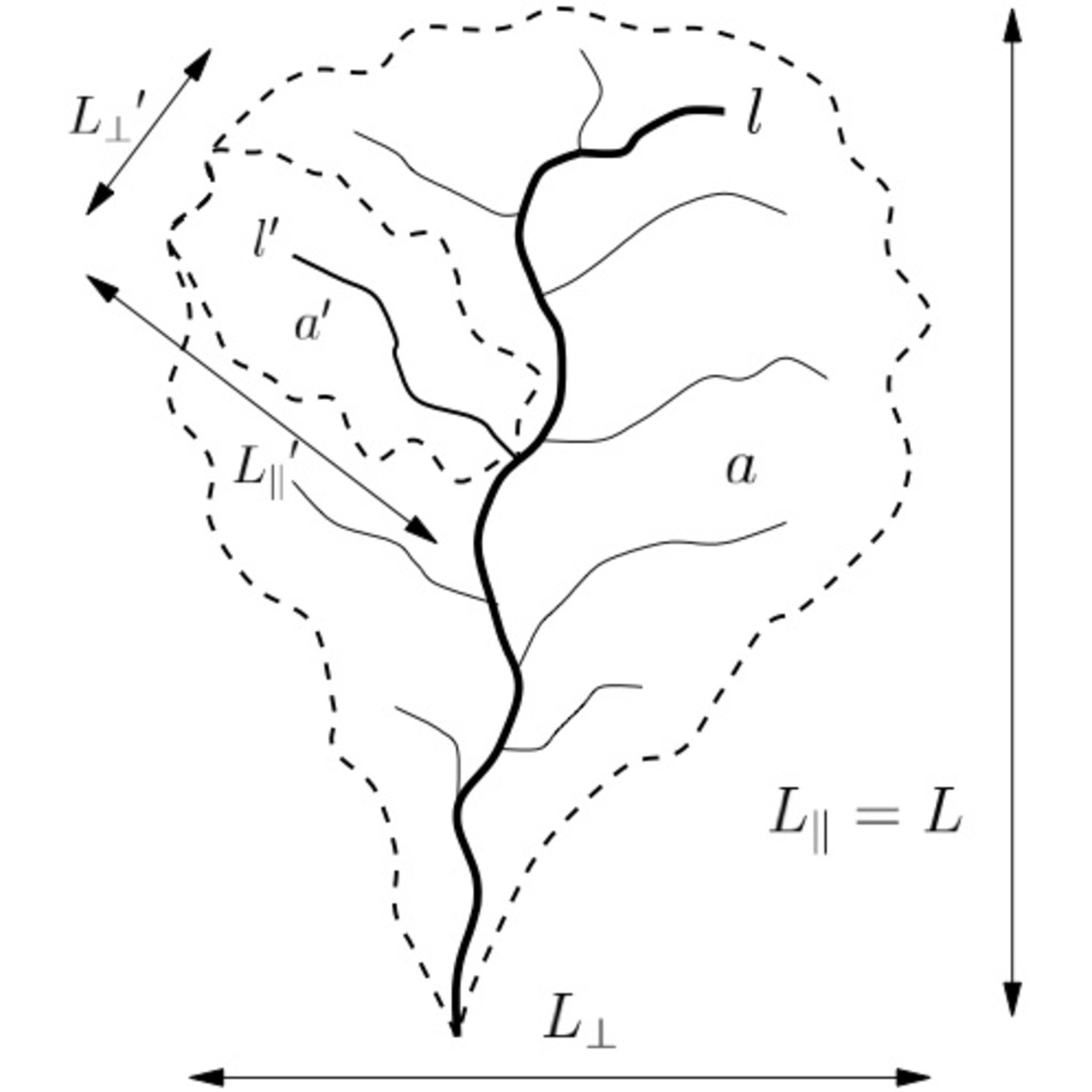
Scaling laws that describe the structure of river networks are shown to follow from three simple assumptions. These assumptions are: (1) river networks are structurally self-similar, (2) single channels are self-affine, and (3) overland flow into channels occurs over a characteristic distance (drainage density is uniform). We obtain a complete set of scaling relations connecting the exponents of these scaling laws and find that only two of these exponents are independent. We further demonstrate that the two predominant descriptions of network structure (Tokunaga's law and Horton's laws) are equivalent in the case of landscapes with uniform drainage density. The results are tested with data from both real landscapes and a special class of random networks.