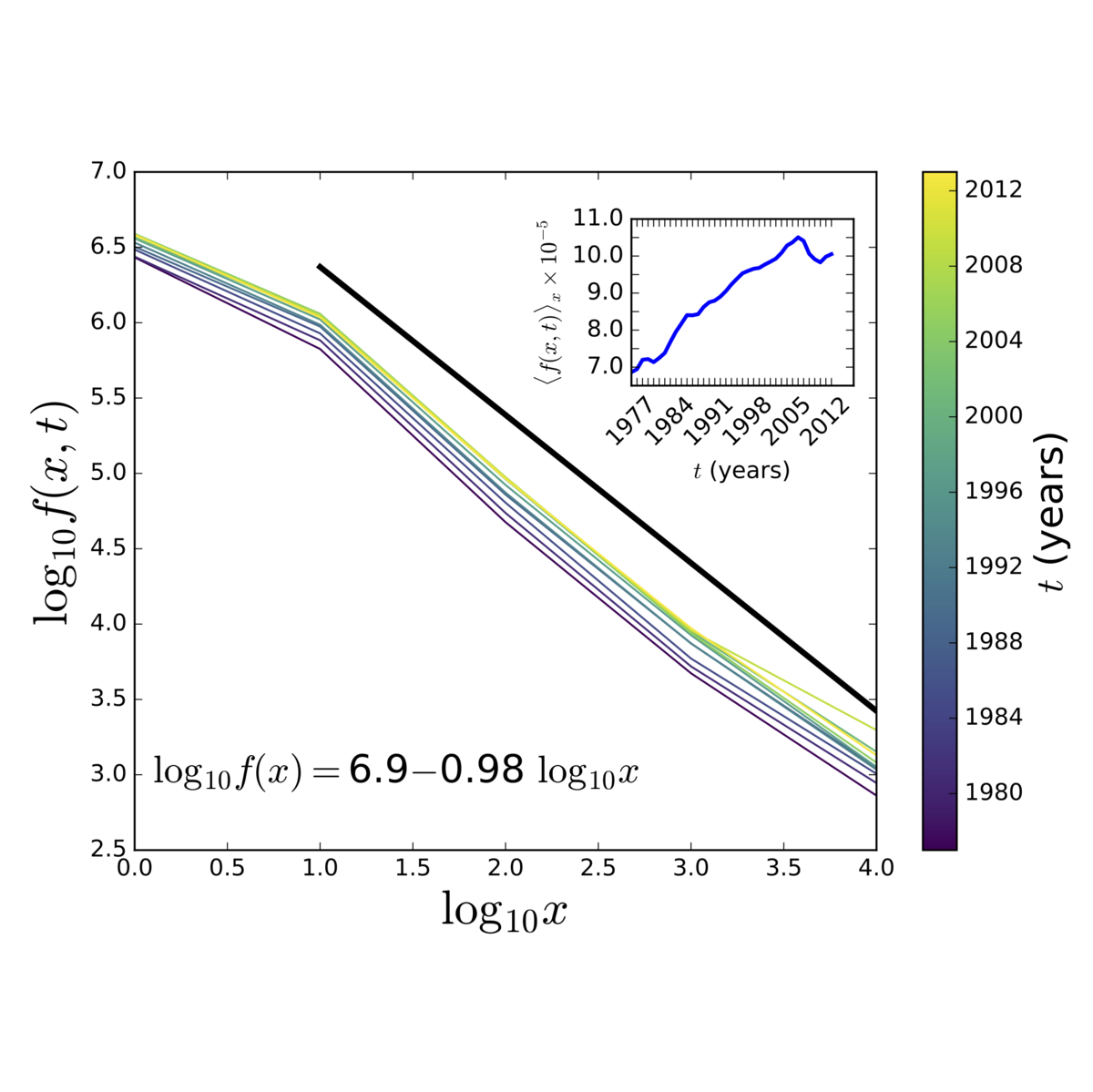
Classical rich-get-richer models have found much success in being able to broadly reproduce the statistics and dynamics of diverse real complex systems. These rich-get-richer models are based on classical urn models and unfold step-by-step in discrete time. Here, we consider a natural variation acting on a temporal continuum in the form of a partial differential equation (PDE). We first show that the continuum version of Herbert Simon's canonical preferential attachment model exhibits an identical size distribution. In relaxing Simon's assumption of a linear growth mechanism, we consider the case of an arbitrary growth kernel and find the general solution to the resultant PDE. We then extend the PDE to multiple spatial dimensions, again determining the general solution. Finally, we apply the model to size and wealth distributions of firms. We obtain power law scaling for both to be concordant with simulations as well as observational data.