Better writing, editing, and thinking through the power of line breaks
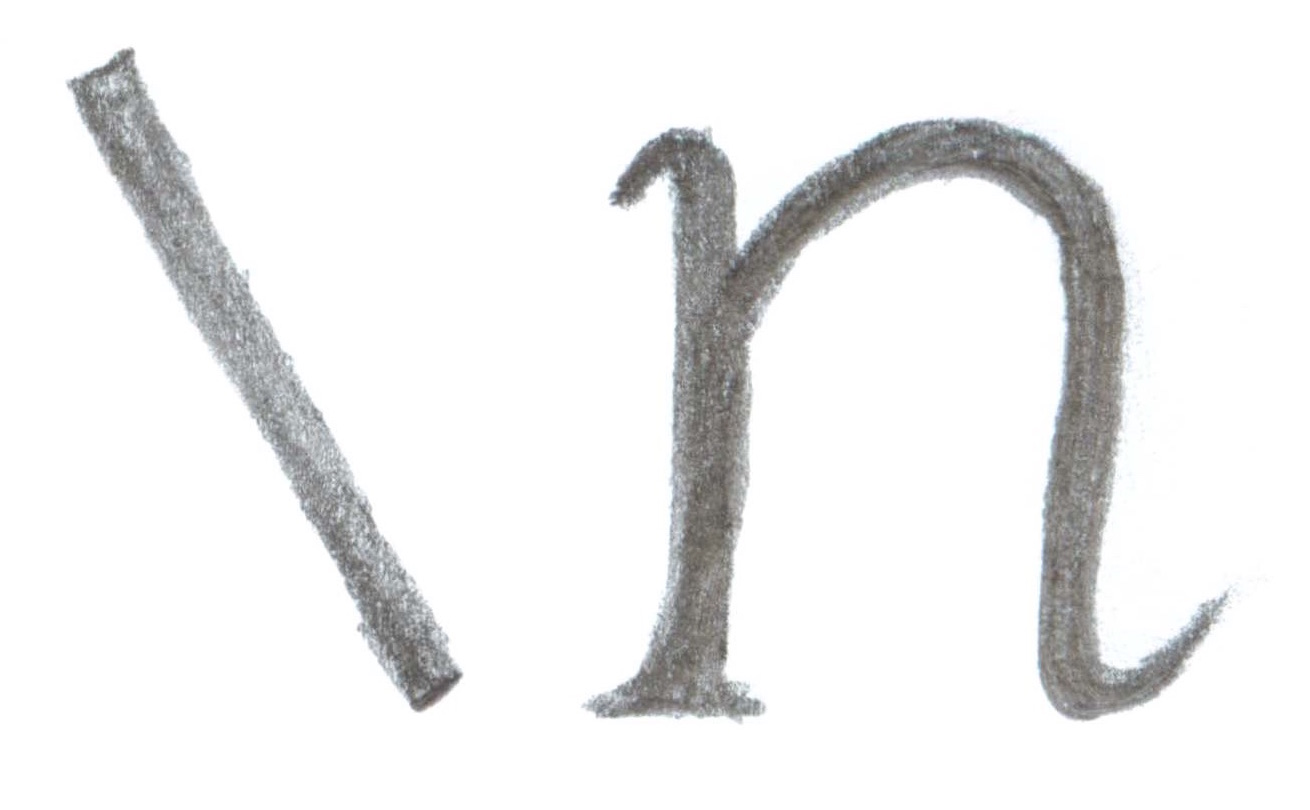
With *LaTeX and markup languages in general, the (partial) separation of content from format allows us to write in ways that are
- Conceptually powerful; and
- Excellently structured for editing (which is when the best writing most often happens).
In this post, I'll provide some of what I find to be good practices for writing *LaTeX documents.
Writing is coding:
A framing first: written text is code—an algorithm intended to elicit specific thinking (which I'll say includes emotion, a fundamental kind of thinking) or a variety of possible thoughts in a reader's mind. With computer programs, we have the clean distinction of human readable/editable code and resultant compiled binaries. For written text, and perhaps surprisingly given we're now talking about people communicating with each other and not machines, being human editable and being human readable are also not exactly the same thing.
Linebreakfulness:
Let's start with a most excellent implement: \n, the line break.
A simple, vital element of writing
enabled by *LaTeX is that we can start each
new sentence or phrase
on a separate line.
(This paragraph provides an example,
even if we're in textwrapping html-space.)
The benefits are that it's then:
- easy to move sentences and phrases around (Emacs and other powerful text editors make this a pleasure); and
- reflective of the actual structure of the thought process that goes into writing. Phrases are a natural base unit, so breaking at commas and semi-colons makes sense, and long phrases should have carriage returns applied liberally. When line breaks are used well, sentences and phrases are clearly rendered as the core material of a text.
Note: Emacs and presumably other editors can be extended to make line breaks occur automatically, and to repack paragraphs with line breaks after each phrase-ending element.
My PhD advisor Dan Rothman pointed out the blocking by sentences idea and, over time, I've found many kinds of *LaTeX structures can be laid out in ways I find better for writing, rewriting, and, inextricably, thinking.
I'll go through an example for equations and then add a few examples of other environments and elements.
Equations:
Here's an initial form of an equation for the Jensen-Shannon divergence from one of our papers on Google Books:
\begin{equation}D_{JS,i}(P||Q) = -m_i\log m_i + \frac12\left(p_i\log p_i+q_i\log q_i\right).\end{equation}
Here's the output which is in decent shape: \begin{equation}D_{JS,i}(P||Q) = -m_i\log m_i + \frac12\left(p_i\log p_i+q_i\log q_i\right).\end{equation}
The LaTeX code is compact, does the job, but is difficult to read and edit. Let's help ourselves (the machines will be fine) and step through some improvements.
First, we need to separate the environment, indent the equation, and add a label for potential referencing:
\begin{equation}
D_{JS,i}(P||Q) = -m_i\log m_i + \frac{1}{2}\left(p_i\log p_i+q_i\log q_i\right).
\label{JSequation}
\end{equation}
I like to add the label at the end of environments
that use them (figures, tables, etc.).
I've also added curly braces to the
\frac command;
\frac{1}{2} is clearer and allows for more complicated
arguments.
As for sentences, we can deploy line breaks to leave
the equation both easier to read and edit.
Here's a simple start:
\begin{equation}
D_{JS,i}(P||Q) =
- m_i \log m_i +
\frac{1}{2}\left(p_i \log p_i + q_i \log q_i \right).
\label{eq:googlebooks.JSequation}
\end{equation}
The main pieces of the equation (blob = blob + blob) now have
their own lines.
But we can do more and break the equation
across lines into its smallest functional units.
We'll do these things:
- Give equalities and operations their own line .
- As for the equation environment, place enclosing bracket structures on separate lines, and allow the editor to indent things nicely.
\begin{equation}
D_{\textrm{JS},i}
(P\,||\,Q)
=
- m_i \log_{2} m_i
+
\frac{1}{2}
\left(
p_i \log_{2} p_i
+
q_i \log_{2} q_i
\right).
\label{eq:googlebooks.JSequation}
\end{equation}
The output has changed in a just a few small ways: \begin{equation} D_{\textrm{JS},i} (P\,||\,Q) = - m_i \log_{2} m_i + \frac{1}{2} \left( p_i \log_{2} p_i + q_i \log_{2} q_i \right). \end{equation} Both reading and editing are now simple. A few notes:
- As for sentences, we can easily move functional units around by cutting lines or sets of lines. If we wanted to swap the order of $p_i \log_{2} p_i$ and $q_i \log_{2} q_i$, we would just cut and paste lines (some C-k, C-y action).
- I've kept the form $p_i \log_{2} p_i$ together as this is a conceptually clear element for entropy.
- $D_{\textrm{JS},i}$ and $(P\,||\,Q)$ are on separate lines to make future editing easier, and we've given the $P$ and $Q$ some breathing room with the small space "\,".
- We've also converted $JS$ to $\textrm{JS}$ so that this subscript is set in normal text rather than math text.
- Last: we've made the $\log$ into $\log_{2}$ to be clear. Again, even when a single term is a subscript or an argument it's best to use curly braces for clarity and future editing.
-
If we use mildly complex expressions even more than
a few times, it's a good idea to turn them into a command.
We may find we have a general structure that could take
in arguments as well.
So for example we could replace
D_{\textrm{JS},i}(P\,||\,Q)with a command\DJS{P}{Q}with
in the preamble (I like to have a separate settings file; more on this elsewhere).\newcommand[2]{\DJS}{ D_{\textrm{JS},i} (#1\,||\,#2) } -
In fact, for any repeated structure, no matter how simple, it's useful
to create a command to simplify wholesale document changes.
For example, if you've been using $d$ for density and decide that
$\rho$ would be a loftier symbol, then search and replace will bring sadness.
Much better to have started off with:
\newcommand{\density}{d}and then be able to move to\newcommand{\density}{\rho}with one simple change. -
Along the way, I created a richer reference description for the label.
As a rule, I use this format:
\label{eq:papertag.tag}
\label{fig:papertag.tag}
\label{tab:papertag.tag}
\label{sec:papertag.tag}
\label{subsec:papertag.tag}
where papertag gives a semantically reasonable pointer to the paper. Having this extra level of identification is useful in various ways including (1) being able to search for a certain kind of reference (e.g., just figures), and (2) when combining documents to form, for example, an edited volume or thesis.
All right. Here's a selection of example formats, including a few more equations:
More Equations:
From our charming paper on Limited Imitation Contagion:
In Fig.~\ref{fig:updownrfn_network02}A,
we show an example of a probabilistic response function,
the tent map, which is defined as
$
T_r(x)
=
rx
$
for
$
0 \le x \le \frac{1}{2}
$
and
$
r(1-x)
$
for
$
\frac{1}{2} \le x \le 1.
$
While breakable, the ranges for $x$ make for reasonable phrases
so they both stay intact on a single line.
Here's the output:
In Fig. 1A, we show an example of a probabilistic response function, the tent map, which is defined as $ T_r(x) = rx $ for $ 0 \le x \le \frac{1}{2} $ and $ r(1-x) $ for $ \frac{1}{2} \le x \le 1. $
From my course Beamerized Principles of Complex Systems, part of a calculation for Herbert Simon's Rich-gets-Richer model:
Preamble (included in a separate settings file):
\newcommand{\avg}[1]{\left\langle#1\right\rangle}
\newcommand{\simonalpha}{\rho}
Calculation:
$$
\avg{N_{k,t+1} - N_{k,t}}
=
(1-\simonalpha)
\left(
(k-1)\frac{N_{k-1,t}}{t}
-
k\frac{N_{k,t}}{t}
\right)
$$
becomes
$$
n_k(t+1)-n_k t
=
(1-\simonalpha)
\left(
(k-1)\frac{n_{k-1}t}{t}
-
k\frac{n_{k}t}{t}
\right)
$$
Output: $$ \newcommand{\avg}[1]{\left\langle#1\right\rangle} \newcommand{\simonalpha}{\rho} \avg{N_{k,t+1} - N_{k,t}} = (1-\simonalpha) \left( (k-1)\frac{N_{k-1,t}}{t} - k\frac{N_{k,t}}{t} \right) $$ becomes $$ n_k(t+1)-n_k t = (1-\simonalpha) \left( (k-1)\frac{n_{k-1}t}{t} - k\frac{n_{k}t}{t} \right) $$
Figures and Tables:
Here's a draft example figure environment, one spanning two columns
in our
PNAS paper on the positivity of human language (Fig. 3). Fairly simple: centre the figure and then give the
caption plenty of linebreakage.
The long figure name and labels are no problem to handle and mitigate the possibility
of overlap later on (note the paper tag mlhap).
Giving figures long names (lumping tags together) makes finding
them later on (if and when one's memory fails) much simpler (using, for example, locate).
Table environments can be laid out in the same way, with
some attention paid to tabular environments.
Some good practices foe structuring work directories will appear elsewhere.
\begin{figure*}
\centering
\includegraphics[width=\textwidth]{fighappinessdist_jellyfish_words_havg_multilanguage_example001_noname.pdf}
\caption{
Examples of how word happiness varies little
with usage frequency.
Above each plot is a histogram of average happiness $h_{\rm avg}$
for the 5000 most frequently used words in the given corpus, matching
Fig.~\ref{fig:mlhap.happinessdist_comparison}.
Each point locates a word by its rank $r$ and average happiness
$h_{\textrm{avg}}$,
and we show some regularly spaced example words.
The descending gray curves of these jellyfish plots
indicate deciles for windows of 500 words of
contiguous usage rank,
showing that the overall histogram's form is
roughly maintained at all scales.
The `kkkkkk...' words represent laughter in Brazilian Portuguese,
in the manner of `hahaha...'.
See
Fig.~\ref{fig:mlhap.jellyfish_translated}
for an English translation, Figs.~\ref{fig:mlhap.happinessdist_jellyfish_words_havg_multilanguage001_table1}--\ref{fig:mlhap.happinessdist_jellyfish_words_havg_multilanguage001_table4}
for all corpora,
and Figs.~\ref{fig:mlhap.happinessdist_jellyfish_words_hstd_multilanguage001_table1}--\ref{fig:mlhap.happinessdist_jellyfish_words_hstd_multilanguage001_table4}
for the equivalent plots for standard deviation of word happiness
scores.
}
\label{fig:mlhap.jellyfish}
\end{figure*}
Okay, that's enough:
Nutshell: line breaks are unexpectedly good friends.
Using them well with sophisticated markup languages will enable faster and (hopefully) better writing and editing.

